컴퓨터의 수 표현

컴퓨터는 우리가 사용하는 10진법의 수를 사용하지 않고 2진법의 수를 사용한다.

모든 컴퓨터의 숫자는 전기 신호이고 과거에는 이러한 전기신호를 구별하기가 어려워 전기신호의 ‘on’ 과 ‘off’를 구별하는 것이 최선이었다. 이후에도 3진법을 사용한 컴퓨터를 연구했지만 2진법을 사용한 컴퓨터가 더 효율이 좋고, 정확성이 높았다.

최근에는 3진법 반도체 구현과 양자 컴퓨터가 개발 중에 있다. 이를 이용한 컴퓨터가 능력이 좋다면 사용하지 않을 이유가 없다.

참고 자료 : https://www.howtogeek.com/367621/what-is-binary-and-why-do-computers-use-it/

정수 표현

일반적으로 컴퓨터에서 사용되는 자료형의 종류이다

이를 C언어 에서는 short, int, long 이라고 사용하여 정수를 저장한다.

파이썬에서는 임의 정밀도 산술을 이용하여 정수를 저장한다

컴퓨터가 양의 정수를 표현하는 경우에는 부호 비트(MSB)를 0으로 놓고, 남은 비트로 2진수를 표현하면 된다.

따라서 표현할 수 있는 가장 큰 32비트 값은 아래와 같다.

0111 1111 1111 1111 1111 1111 1111 1111b (7FFFFFFFx) = 214748364

번외) 값을 메모리에 저장하는 법

메모리에서는 정수 데이터를 저장하기 위해 4칸을 사용한다. byte는 컴퓨터가 정보를 저장하는 가장 작은 단위이자 메모리 상에서 주소가 배정될 수 있는 가장 작은 단위이다. 메모리는 바이트 단위로 주소가 배정되어 있고(주소가 배정되어 있어야 접근이 가능하다). 정수는 4바이트이므로 4칸(32bit)이 필요하다. 이 4칸의 메모리에 정수를 어떤 순서로 저장하냐에 따라 Big Endian, Little Endian으로 분류할 수 있다.

파이썬에서는 변수에 값을 할당하면 object를 생성해서 값을 해당 객체에 저장한 후 변수는 해당 객체의 메모리 주소를 의미하는 id 값을 가지게 된다

파이썬에서 변수의 값은 배정문(=)에 의해 부여되며 다음 배정문은 x의 주소에 값 20을 저장한다는 의미이다

x = 20

그리고 다음 배정문은 y에 x의 값을 저장한다는 것을 의미한다

y = x

여기에서 x와 y는 모두 변수 이름임에도 불구하고 배정문 왼쪽의 y는 주소를 의미하고, 오른쪽은 x는 x의 값을 의미한다.

번외) 임의 정밀도

임의 정밀도 정수형이란 쉽게 말해 무제한 자릿수를 제공하는 정수형을 말한다.

정수를 숫자의 배열로 간주하여, 자릿수 단위로 쪼개어 배열 형태로 표현한다.

파이썬은 10진수를 230진수로 변경하여 한 자리수가 나타낼 수 있는 최대값은 230 - 1 이다. 플랫폼에 따라 파이썬은 30비트의 자리수를 가진 32비트의 부호 없는 정수 배열 또는 15 비트의 자리수를 가진 16 비트의 부호 없는 정수 배열을 사용한다.

123456789101112131415의 표현식은 다음과 같다:

(437976919 * 2**(30*0)) + (87719511 * 2**(30*1)) + (107 * 2**(30*2))
a = (437976919 * 2**(30*0))
b = (87719511 * 2**(30*1))
c = (107 * 2**(30*2))

print(a + b + c)

123456789101112131415

참고자료 : https://rushter.com/blog/python-integer-implementation/

참고자료 : https://mingrammer.com/translation-cpython-internals-arbitrary-precision-integer-implementation/

음수 표현

컴퓨터에서 음수를 표현하는 방법은 여러 종류가 있다.

1) 부호화 크기 방법 (Signed Magnitude)

최상위 비트(MSB)를 부호로 사용하는 것.

최상위 비트가 0이면 양수 1이면 음수로 표현한다. (0000 0001b = 1), (1000 0001b = -1)

하지만 이는 +0(0000 0000b)과 -0(1000 0000b)이라는 0이 두 개 존재하는 문제가 있고, 양수와 음수 간의 연산이 어렵다.

5 - 5 연산의 경우

5 + (-5) = 00000101b + 10000101b = 10001010b = -10 

이라는 답이 나온다

2) 2의 보수를 사용하는 방법 (2’s Complement)

보수란 각 자리의 숫자의 합이 어느 일정한 수가 되게 하는 수이다. 2진수에는 숫자의 합이 1이 되는 1의 보수법과 1의 보수법에 +1을 시켜주는 2의 보수법이 있다.

십진수 5는 이진수로 0000 0101b 이고 이를 1의 보수법으로 표현하면 1111 1010b이다. 여기에 +1을 하면 1111 1011b로 2의 보수법으로 표현할 수 있다. 이는 십진수 251의 값인데, 2의 보수법에서는 251을 -5로 표현한다.

8bit 포맷의 경우 표현 가능한 숫자 범위가 0 ~ 255인데, 그 반인 127(0111 1111b)까지는 양수, 128(1000 0000b)부터는 거꾸로 음수 -128로 표현하는 것이다.

이럴 경우 나타낼 수 있는 가장 작은 수는

11111111b = -1

이므로 -0을 표현하는 오류가 발생하지 않는다

예를 들어 10 - 3 을 보수법으로 계산할 경우 10은 0000 1010b이고 -3은 0000 0011b에서 2의 보수법을 사용하여 1111 1101b이 된다 이 둘을 더할 경우

10 + (-3) = 00001010b + 11111101b = 100000111b = 7

맨 앞자리 1을 제외하면 7이라는 값이 나온다.

실수 표현

1) 고정 소수점(Fixed Point) 방식

32bit의 수인 경우 언제나 1비트를 부호 , 15비트를 정수, 16비트를 소수 표현에 사용하는 식이다.

부호와 정수부, 소수부를 표현하는 부분의 크기가 고정되어 있어서 실수 표현 범위가 넓지 않다.

2) 부동 소수점(Floating Point) 방식

컴퓨터에서 사용하는 부동 소수점 표기법은 IEEE 754 표현법을 따른다.

• 부호 비트(signed bit) : 최상위 1bit로 0(양수), 1(음수) 값을 갖는다.
• 지수(exponent) : 7bit로 수의 표현 범위를 나타내며, 지수에 의해서 소수점이 이동한다
• 가수(fraction) : 양의 정수로 나타낸 근사치를 나타내며, 정밀도에 따라 다르다

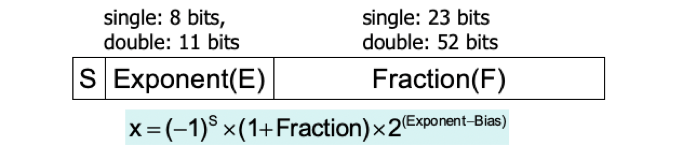
x = [(-1) ** (부호 비트)] * (1 + 가수) * [2**(지수 + 바이어스)]
												정규화된 지수 = 1

-118.625 를 IEEE 754 로 표현할 경우.

음수이므로 부호 비트는 1이 된다.

그 다음, 118은 1110110b 이고 0.625는 0.101b가 된다. 둘을 합하면 1110110.101b이다

소수점을 왼쪽으로 이동시켜, 왼쪽에는 1만 남게 만든다.

1110110.101 = 1.110110101 << 6 = 1.110110101 * 2**6 

이것을 정규화된 부동소수점 수라고 한다.

• 정규화란

  가수의 첫째 자리가 밑수보다 작은 한자리 자연수가 되도록 바꾸는 것

가수부는 소수점의 오른쪽 부분으로, 부족한 비트 수 부분만큼 0으로 채워 23비트로 만든다.

지수는 6이므로, bias를 더해야 한다. 32비트 IEEE 754 형식에서는 Bias는 127이므로 6 + 127 = 133 이 된다. 133 = 10000101b가 된다.

[(-1) ** (부호 비트)] * (1 + 가수) * [2**(지수 + 바이어스)]
1 10000101 1101101010...b -118.625
부호비트 | 지수 + 바이어스 | 정규화된 가수
-118.625
- | 118 + 0.625
- | 1110110.101b
- | 1.110110101b * 2**6 == 1.110110101b << 6
- | 6(2의 지수)  + 127(바이어스) == x | 1.1101101010...b (정규화된 가수)
- | 133(x) | 1.1101101010...b
- | 10000101 | 1.1101101010...b
1 | 10000101 | 1101101010...b

참고자료 : https://dheldh77.tistory.com/entry/Floating-Point-Number

IEEE 부동소수점 표시의 목적은 정수와 같은 32bit를 사용하여 실수를 표현하기 위해서이다.

• 익세스 표현법 (Excess Notation). 익세스 표현법은 지수부에서 나타낼 수 있는 최대값을 절반으로 나누고 그 값을 0으로 바꾼 뒤에 그것을 부호와 크기를 나타내는데 사용하는 방법이다 단정도 실수의 경우 지수부분에 8비트를 사용한다 8비트의 최대값은 십진수로 255 이진수로 1111 1111b이다 이의 절반 127, 0111 1111b은 익세스 표현법상 0을 나타낸다 이를 바이어스(bias)라고 부른다

0000 0000b : -127
0000 0001b : -126
...
0111 1111b : 0
...
1111 1111b : 127 == 바이어스 상수

• 단정도(Single Precision) 표현 방식

  유효숫자가 7개이다

  32bit 값을 사용한다

• 배정도(Double Precision) 표현방식

  유효숫자가 16개이다

  64bit 값을 사용한다

음수를 표현할 때 왜 2의 보수법이 아니라 익세스 표현법을 사용할까?

각각의 방식으로 십진수를 표현할 경우 2의 보수법은 순서가 도중에 바뀐 형태로 나타나지만 익세스 표현법의 경우 보이는 수의 크기와 실제 수의 크기가 순서대로 나타난다.

2의 보수법으로 나타낸 -3 = 1111 1101b
2의 보수법으로 나타낸 3 = 0000 0011b
익세스 표현법으로 나타낸 -3 = 0111 1100b
익세스 표현법으로 나타낸 3 = 1000 0011b

지수에 대해 2의 보수법을 사용한 경우 두 번째 MSB가 부호에 의해 정해지므로 작은 음수는 매우 큰 정수처럼 보인다. 대신 익세스 표현법을 사용하면 크기가 순서대로 나타난다.

참고자료 : https://stackoverflow.com/questions/2835278/what-is-a-bias-value-of-floating-point-numbers